Obverse (l) and reverse (r) of a geometric word-problem text (IM 121613. Image courtesy CDLI)

Cuneiform Mathematics: Outstanding Techniques in a System of Texts

February 2023 | Vol. 11.2

By Carlos Gonçalves

Mathematical cuneiform documents from various sites and periods provide a wealth of information about the conceptualization and practice of mathematics in ancient Mesopotamia. The corpus is especially rich for the Old Babylonian period (ca. 1900 – 1600 BCE), and from these documents we can observe a systematic approach to the transmission of mathematical knowledge and tools.

The most common evidence for mathematical knowledge in ancient Mesopotamia is given by cuneiform tablets that were used in the teaching and learning process, either in a school itself, or, as might be the case of the so-called advanced mathematics, some erudite environment connected to the schools. Another category of evidence is given by cuneiform documents that integrated professional practice: the planning of a canal, loan contracts, inventories, and land-division diagrams are documents whose effectiveness depended on skills in counting, measuring, calculating, and doing geometry. Indirect evidence also comes from material culture that reflects the application of mathematical calculations, such as buildings, irrigation networks, the fabrication of bricks, the division of work, and the distribution of food rations. To all this, we could add what became known as “eduba texts”: narratives which portray the life within the schools in Mesopotamia, especially in the Old Babylonian period, giving an important place to mathematics.

Although mathematics must have existed in Mesopotamia also as knowledge that was orally developed, transmitted, and adapted, historians unfortunately don’t have direct access to such traditions. In the best of scenarios, we may have only glimpses of mathematical orality from the traces it left in the written word, but so far no systematic research work has been done in this direction. Having said that, the historiography of cuneiform mathematics has been enormously fruitful in analyzing the surviving texts, such that countless aspects of the outstanding Mesopotamian mathematical techniques are known today.

More impressively, however, we know Mesopotamians were able to organize this amazing knowledge not in an abstract mathematical treatise as in some other mathematical traditions, but in a system of mathematical textual genres, which will be briefly sketched out in the following.

The first genre consists of multiplication tables, which were very common in Old Babylonian scribal schools, such as in this tablet in the Louvre (AO 8901):

Figure 1: Obverse of an Old-Babylonian multiplication tablet (Louvre AO8901). Photograph by author.

A multiplication table usually consisted of the results of the multiplication of a fixed number by the factors from 1 to 20 and by 30, 40, and 50. As each multiplication table was relative to only one fixed number, students had to learn several of them, each one for a different fixed number. The fixed number is called the “head number” in Assyriological publications. In the case of AO 8901, the head number is written in cuneiform as in Fig. 2, corresponding to the two slightly damaged initial cuneiform signs in the first line of the tablet:

Figure 2: Reconstruction of the damaged beginning of the first line of the above tablet: a cuneiform representation of the value “7:30” (= 450 in our system).

The seven vertical wedges at the left represent seven units, while the three wedge-heads at the right (called “Winkelhaken” in Assyriological texts) represent three tens. Together, scholars annotate this as “7:30”. AO 8901 shows the results of the multiplications of 7:30 by the factors 1 to 20, and by 30, 40, and 50.

Numbers in multiplication tables followed a sexagesimal system (aka base 60). We still use the sexagesimal system for counting time, so “7:30” can be roughly understood as 7:30 in a clock display, i.e. 7 units of 60, plus 30:

7:30 = 7 x 60 + 30 = 450

In other words, 7:30 in base sixty is the same as 450 in base 10.

Figure 3: Some columns of the cylinder A 7897 in the Oriental Institute (Image courtesy the Oriental Institute).

One interesting thing is that there was no fixed order of magnitude when numbers were written in the sexagesimal system. To keep with the comparison with the clock display, it is as if 7:30 could represent 7 hours and 30 minutes or 7 minutes and 30 seconds, with context as the only criterium to help decide which option is the correct one.

When students in a scribal school had committed to memory several multiplication tables with different head numbers, they could produce a different type of text which we refer to as a composite multiplication table, because it is the result of the juxtaposition of several multiplication tables one after the other on one same writing surface. An example of this is on the clay cylinder A 7897, held in the collection of the Oriental Institute in Chicago (See Fig. 3). Its columns contain a long series of individual multiplication tables (See Fig. 4). Multiplication tables like AO 8901 and composite multiplication tables like A 7897 are different textual genres integrating the system Mesopotamians developed to organize their mathematics.

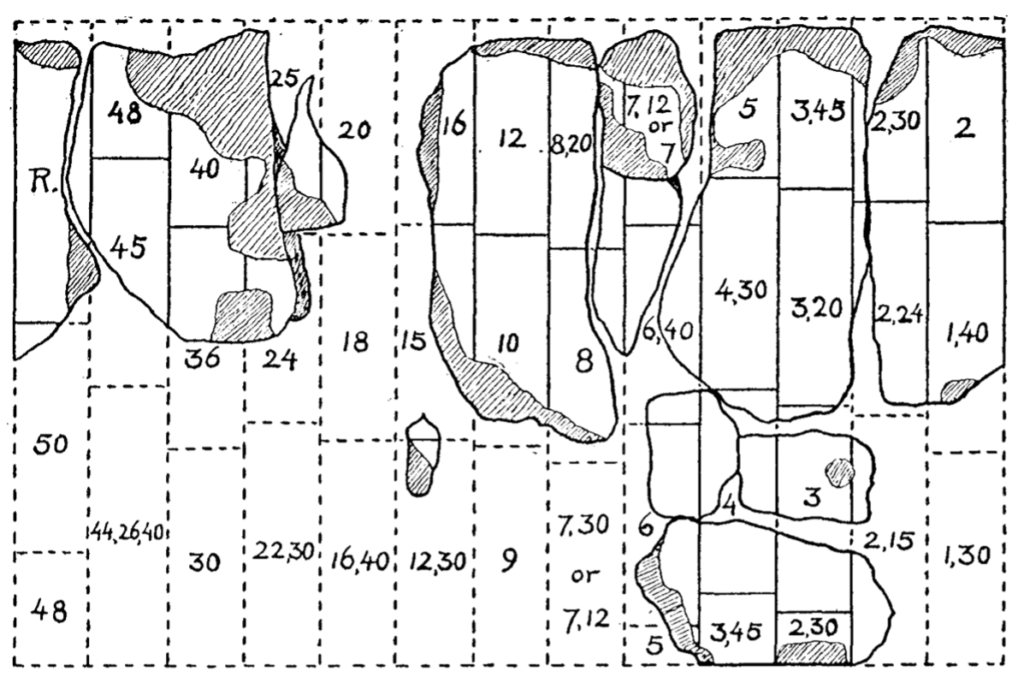
Figure 4: Schematic drawing of cylinder A 7897, showing only the head numbers of the multiplication tables written on its surface.(Neugebauer and Sachs 1945, 25).

Another type of table is called a metrological table, because it deals with measurement values. Each of its lines associates a measurement value and a sexagesimal number. This allowed scribes to carry out various types of practical computations involving units of measure. In the example below from the Diyala region (Oriental Institute A 21948), its lengthy text related surface measurements and sexagesimal numbers.

Its first lines use the surface measurement sar, (approximately 36 square meters) which in the Old Babylonian Period was defined as a square of sides 1 ninda (approximately 6 meters). From the analysis of the parts of the text that are not damaged and from what is known about other similar texts, the complete contents of this metrological table can be reconstructed. Here is how we can understand the first four lines:

Figure 5 (left): Obverse and reverse of a tablet with a metrological table (Oriental Institute A 21948). Image courtesy CDLI.

Figure 6 (right): Drawing of above tablet (Greengus 1979 Plate XCVIII; highlighted by author).

The first lines of A 21948 (highlighted in Figure 6) and what they mean.

Back to the analogy with a clock display, if one third of a sar is associated with 20 (think of 20 minutes), then one entire sar will be associated to 20 times 3, which is exactly 1 (for 60 minutes = 1 hour), as stated in A 21948.

Although metrological tables are a textual genre different from multiplication tables and composite multiplication tables, the concept of multiplication is present in all these types of texts. Mesopotamians went into a high degree of detail in organizing their mathematics.

A fourth type of mathematical textual genre consists of word-problems. Different from mere exercises, word-problems require skill in interpreting the given data, in order to apply mathematics and obtain what is required. A tablet in the collection of the Iraq Museum (IM 121613) contains a sequence of geometrical word-problems, or problem statements and solutions. The first word-problem of this tablet asks for the length and width of a rectangle, if it is known that:

1. Its width is two-thirds of its length and

2. Its surface is six hundred sar

Figure 7: Obverse (l) and reverse (r) of a geometric word-problem text (IM 121613. Image courtesy CDLI)

What is interesting, and this is in fact very common in Old Babylonian word-problems, is how the associations between measurement values and sexagesimal numbers are present in the solution, thus providing a connection between word-problems and metrological tables. As a concrete example, in the first problem of IM 121613, the surface of the rectangle, given as 600 sar, is also referred to as the sexagesimal number 10. In fact, six hundred sar corresponds to the sexagesimal number 10 in tables of surfaces, exemplified by the metrological tablet in figures 5 and 6 (think of 10 hours = 600 minutes).

The four genres briefly sketched out here—multiplication tables, composite multiplication tables, metrological tables and word problems—plus other types not mentioned, formed an interconnected web of textual genres that materialized mathematical knowledge. We now know that this interconnection seems to have had regional variation. In the south of Old Babylonian Mesopotamia, around Nippur, the system worked in a rigid way, with some arithmetical operations being carried out only with sexagesimal numbers. On the other hand, practices in the Diyala region were a bit less rigid, and measurement values could be used for the same operations. Despite these slight differences in what could be called “cultures of computation”, the system of textual genres remained, giving a sense of unity for the Mesopotamian mathematical knowledge.

Carlos Gonçalves is Associate Professor in the Laboratory of the Ancient Near East of the University of São Paulo. He is the author of Mathematical Tablets from Tell Harmal (Springer, 2015).

Further reading:

K. Chemla and C. Michel (eds). 2020. “Mathematics, Administrative and Economic Activities in Ancient Worlds”, (Springer).

K. Chemla, A. Keller, and C. Proust, (eds). 2022 “Cultures of Computation and Quantification in the Ancient World”, (Springer).

C. Gonçalves. 2020 “Notes on the History of the Historiography of Cuneiform Mathematics”, in Perspectives on the History of Ancient Near Eastern Studies (Eisenbrauns/Penn State Univ. Press, pp 147-171).

C. Gonçalves 2022. “Quantification and Computation in the Mathematical Texts of Old Babylonian Diyala”, in Chemla, Keller, and Proust 2022, pp. 691-730.

S. Greengus. 1979. “Old Babylonian Tablets from Ishchali and Vicinity” (Nederlands Instituut voor het Nabije Oosten).

C. Proust. 2007. “Tablettes mathématiques de Nippur” (Institut français d’études anatoliennes Géorge Dumézil & De Boccard).

E. Robson. 2008. “Mathematics in Ancient Iraq. A Social History” (Princeton Univ. Press).

How to cite this article

Gonçalves, C. 2023. “Cuneiform Mathematics: Outstanding Techniques in a System of Texts.” The Ancient Near East Today 11.2. Accessed at: https://anetoday.org/goncalves-cuneiform-mathematics/.